Python

The art of war-python-II

The art of war-python-II

Posted by Kgod on May 6, 2019
次浏览
  • 五、排序与搜索
    • 5-01 排序算法的稳定性
    • 5-02 冒泡排序及实现
    • 5-03 选择排序算法及实现
    • 5-04 插入排序
    • 5-05 希尔排序
    • 5-06 快速排序
    • 5-07 归并排序
    • 5-08 二分查找
  • 六、树和树的算法
    • 6-01 树的概念
    • 6-02 二叉树的概念
    • 6-03 二叉树的广度优先遍历
    • 6-04 二叉树的实现
    • 6-05 二叉树的先序、中序、后序遍历
    • 6-06 二叉树由遍历确定一棵树

五、排序与搜索

排序算法（Sorting algorithm）是一种能将一串数据依照特定顺序进行排列的一种算法。

5-01 排序算法的稳定性

稳定性：稳定排序算法会让原本有相等键值的纪录维持相对次序。也就是如果一个排序算法是稳定的，当有两个相等键值的纪录R和S，且在原本的列表中R出现在S之前，在排序过的列表中R也将会是在S之前。简单来说,如下:
(4, 1) (3, 1) (3, 7)（5, 6）
排序后:
(3, 1) (3, 7) (4, 1) (5, 6) （维持次序）
(3, 7) (3, 1) (4, 1) (5, 6) （次序被改变）

5-02 冒泡排序及实现

  • 冒泡排序（Bubble Sort）是一种简单的排序算法。它重复地遍历要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
  • 冒泡排序算法的运作如下：
    • 比较相邻的元素。如果第一个比第二个大（升序），就交换他们两个。
    • 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
    • 针对所有的元素重复以上的步骤，除了最后一个。
    • 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

  • 冒泡排序的分析
    交换过程图示(第一次)：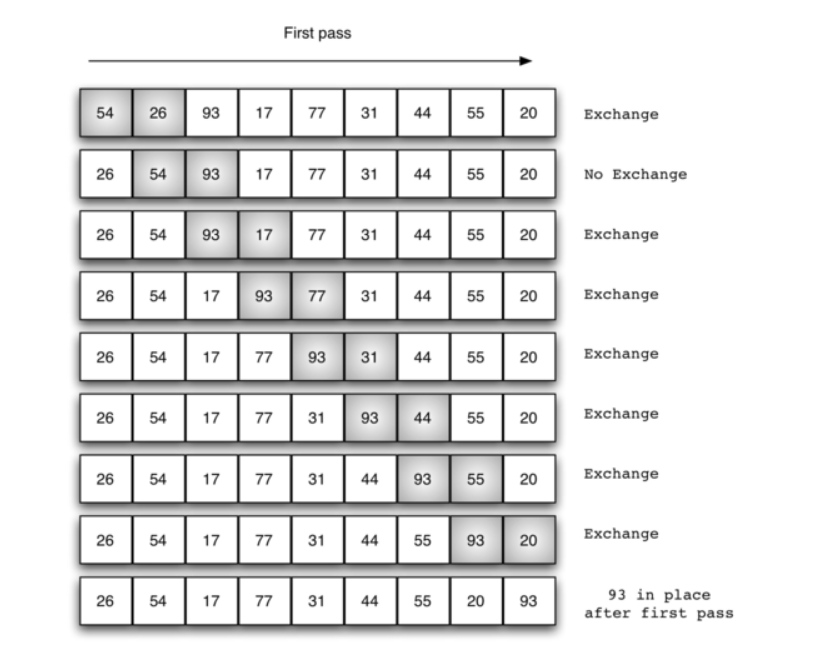
    那么我们需要进行n-1次冒泡过程，每次对应的比较次数如下图所示：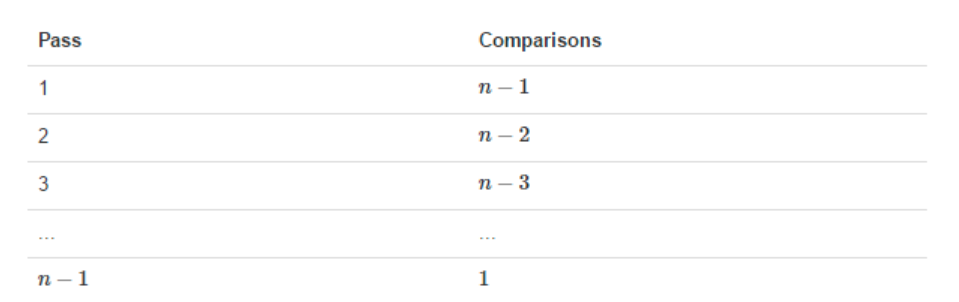

  • 实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

def bubble_sort(alist):
    """冒泡排序"""
    n = len(alist)
    for j in range(n-1):
        #控制循环次数
        
        count = 0 #优化

        for i in range(0,n-1-j):
            #班长从头走到尾
            if alist[i] > alist[i+1]:
                alist[i],alist[i+1] = alist[i+1],alist[i]
                count += 1
        if count == 0:
            #为0说明顺序对的,直接退出
            return

# i 0 ~ n-2   range(0, n-1) j=0
# i 0 ~ n-3   range(0, n-1-1) j=1
# i 0 ~ n-4   range(0, n-1-2) j=2
# j=n   i   range(0,n-1-j)
if __name__ == "__main__":
    li = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    print(li)
    bubble_sort(li)
    print(li)
  • 时间复杂度:
    • 最优时间复杂度：O(n) （表示遍历一次发现没有任何可以交换的元素，排序结束。）
    • 最坏时间复杂度：O($n^2$)
    • 稳定性：稳定
  • 演示:

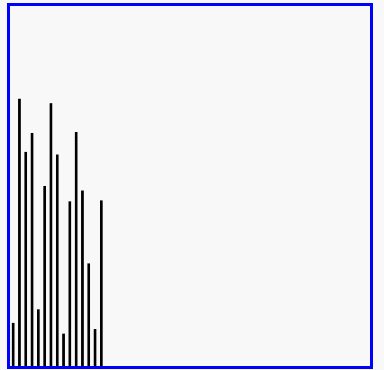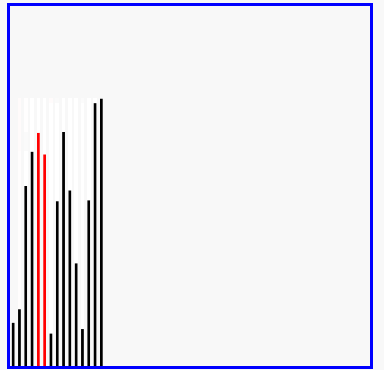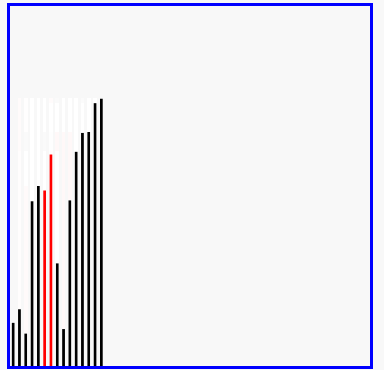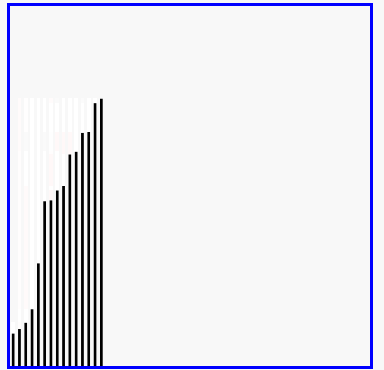
5-03 选择排序算法及实现

  • 选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理如下:首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

  • 选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上，则它不会被移动。选择排序每次交换一对元素，它们当中至少有一个将被移到其最终位置上，因此对n个元素的表进行排序总共进行至多n-1次交换。在所有的完全依靠交换去移动元素的排序方法中，选择排序属于非常好的一种。

-选择排序分析 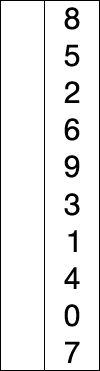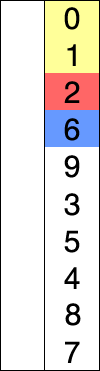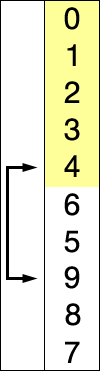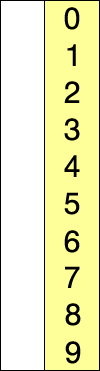红色表示当前最小值，黄色表示已排序序列，蓝色表示当前位置。

  • 实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

def select_sort(alist):
    """选择排序"""
    n = len(alist)
    for j in range(0,n-1):
        #记录最小值的索引
        min_index = j
        for i in range(j+1,n):
            #i 比min_index还小
            if alist[i] < alist[min_index]:
                #记录最小位置
                min_index = i
        #交换
        alist[j],alist[min_index] = alist[min_index],alist[j]


if __name__ == "__main__":
    li = [9 , 16, 17, 15, 11, 26 ]

    print(li)
    select_sort(li)
    print(li)
  • 时间复杂度:
    • 最优时间复杂度：O($n^2$)
    • 最坏时间复杂度：O($n^2$)
    • 稳定性：不稳定（考虑升序每次选择最大的情况）
  • 演示:

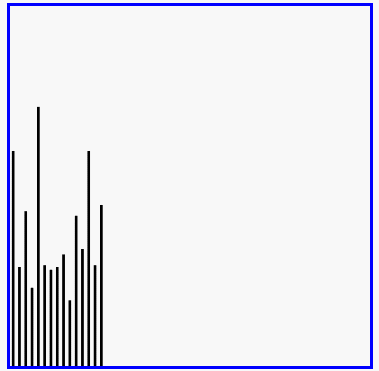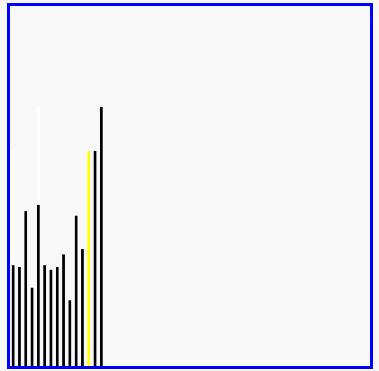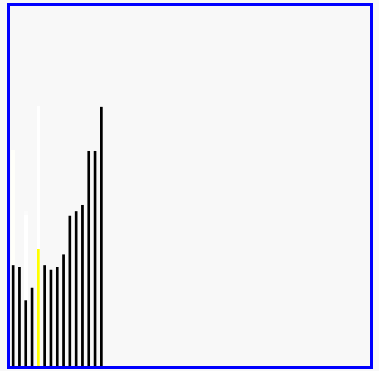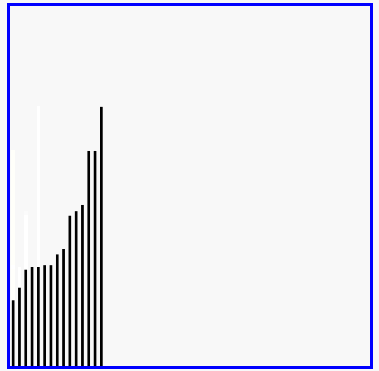
5-04 插入排序

  • 插入排序（Insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。
  • 插入排序分析
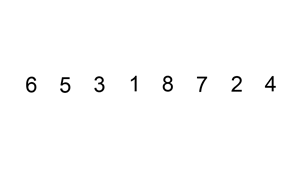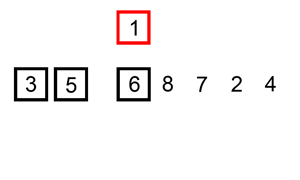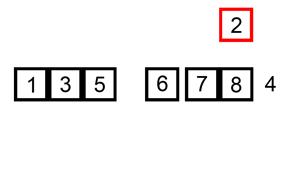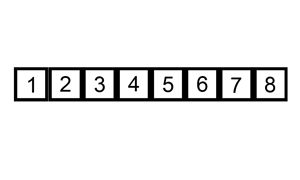
  • 实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def insert_sort(alist):
    """插入排序"""
    # 从右边的无序序列中取出多少个元素执行这样的过程
    n = len(alist)
    for j in range(1,n):
        # j = [1,2,3,...,n-1]
        # i = [1,2,3,...,n-1] 代表内层循环起始值
        i = j
        # 执行从右边的无序序列中取出第一个元素i 然后插入到正确位置中
        while i > 0:
            if alist[i] < alist[i-1]:
                alist[i],alist[i-1] = alist[i-1],alist[i]
                i -= 1
            # 优化
            else:
                break
        # i=j j-1 j-2 ... 1   range(j,0,-1)

if __name__ == "__main__":
    li = [9 , 16, 17, 15, 11,     26    ]

    print(li)
    insert_sort(li)
    print(li)
  • 时间复杂度:
    • 最优时间复杂度：O($n$)
    • 最坏时间复杂度：O($n^2$)
    • 稳定性：不稳定（考虑升序每次选择最大的情况）
  • 演示:

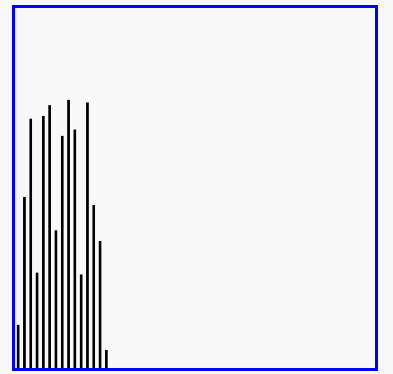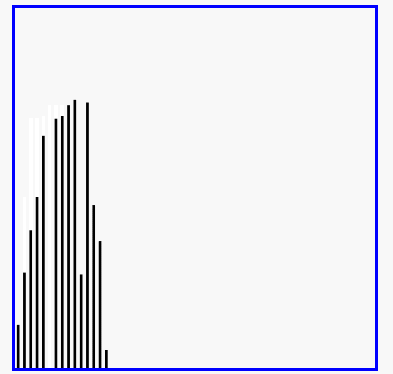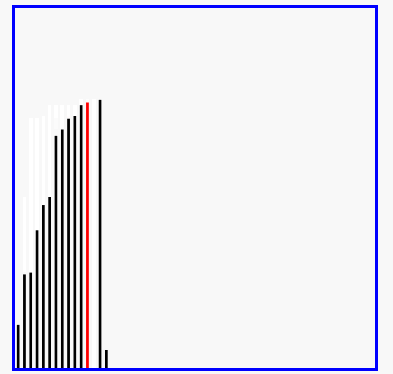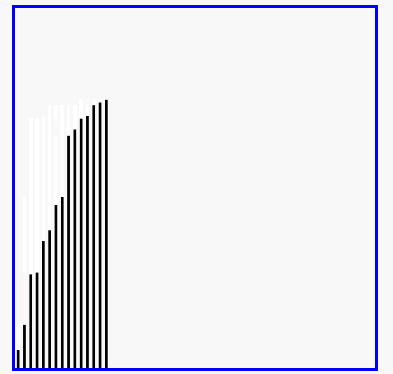
5-05 希尔排序

  • 希尔排序(Shell Sort)是插入排序的一种,也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。 希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

  • 希尔排序过程 希尔排序的基本思想是：将数组列在一个表中并对列分别进行插入排序，重复这过程，不过每次用更长的列（步长更长了，列数更少了）来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法，算法本身还是使用数组进行排序。

例如，假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长为5开始进行排序，我们可以通过将这列表放在有5列的表中来更好地描述算法，这样他们就应该看起来是这样(竖着的元素是步长组成)：

1
2
3
4

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后我们对每列进行排序：

1
2
3
4

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

将上述四行数字，依序接在一起时我们得到：[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ]。这时10已经移至正确位置了，然后再以3为步长进行排序：

1
2
3
4
5
6

10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45

排序之后变为:

1
2
3
4
5
6

10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94

最后以1步长进行排序（此时就是简单的插入排序了）

  • 希尔排序分析

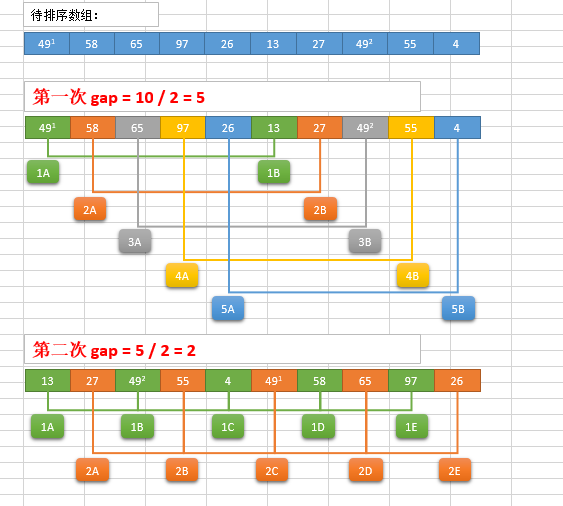
  • 实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

#
#File Name:12-shell_sort.py
#Author:Kgod
#Email:17621512033@163.com
#Homepage:https://aaakgold.github.io
#Create Date:2019-05-13 12:05:56
#Last Modified:2019年05月13日 星期一 12时52分21秒
#Description:
#/

def shell_sort(alist):
    """希尔排序"""
    n = len(alist)
    gap = n // 2
    while gap > 0:
        for j in range(gap,n):
            i = j
            while i >= gap: 
                if alist[i] < alist[i-gap]:
                    alist[i],alist[i-gap] = alist[i-gap],alist[i]
                else:
                    break
                i -= gap
        gap = gap // 2

if __name__ == "__main__":
    li = [-55,77,0.4,9 , 16, 17, 15, 11, 26,99 ]

    print(li)
    shell_sort(li)
    print(li)
  • 时间复杂度:
    • 最优时间复杂度：根据步长序列的不同而不同
    • 最坏时间复杂度：O(n2)
    • 稳定想：不稳定
  • 演示:

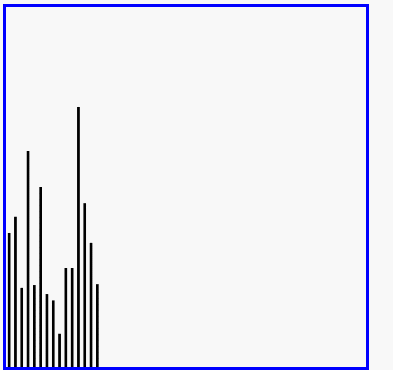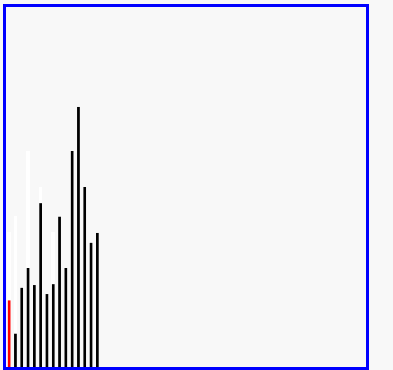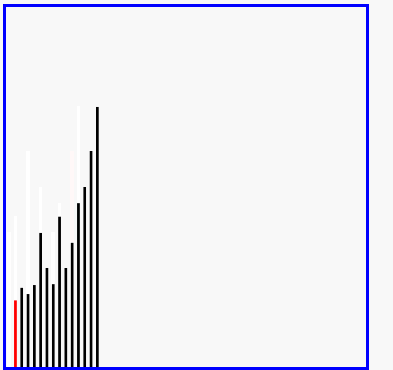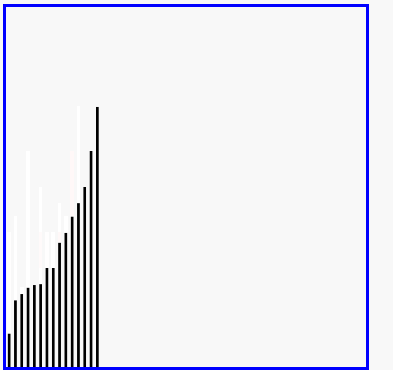
5-06 快速排序

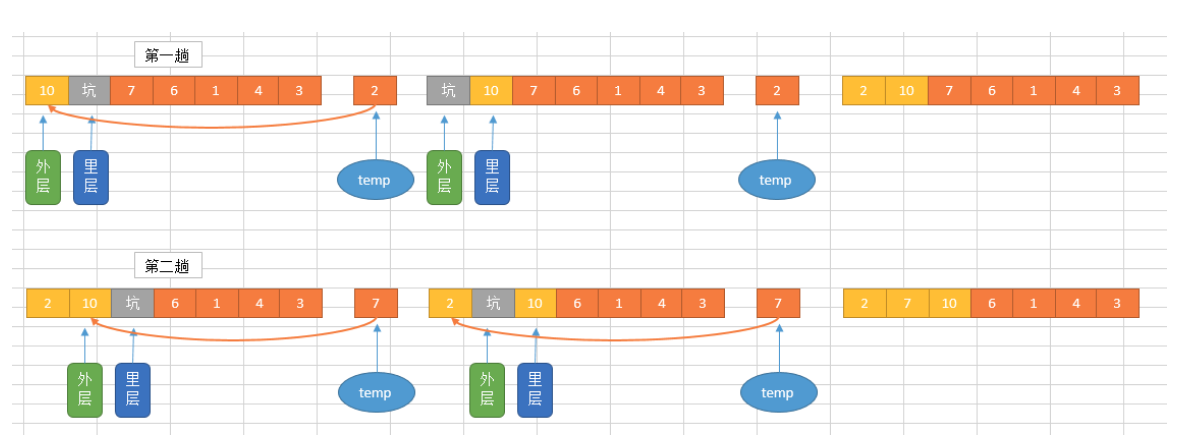
  • 快速排序（Quicksort），又称划分交换排序（partition-exchange sort），通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

  • 快速排序步骤：
    1. 从数列中挑出一个元素，称为”基准”（pivot）.
    2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作.
    3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序.
      递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

  • 快速排序分析:

  • 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

def quick_sort(alist,first,last):
    """快速排序"""
    if first >= last:
        return
    mid_value = alist[first]
    low = first
    high = last
    while low < high:
        # high左移
        while low < high and alist[high] >= mid_value:
            high -= 1
        alist[low] = alist[high]
        # low += 1 此段无需执行,因为上一个while导致下一个while条件肯定满足,low += 1 已经执行
        # low右移
        while low < high and alist[low] <mid_value:
            low += 1
        alist[high] = alist[low]
        # high -= 1
    # 循环退出,low == high
    alist[low] = mid_value
    
    # 对low左边列表排序
    quick_sort(alist,first,low-1)

    # 对low右边列表进行排序
    quick_sort(alist,low+1,last)

if __name__ == "__main__":
    li = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    print(li)
    quick_sort(li, 0, len(li)-1)
    print(li)
  • 时间复杂度
    • 最优时间复杂度：O($nlogn$)
    • 最坏时间复杂度：O($n^2$)
    • 稳定性：不稳定
  • 快速排序演示

5-07 归并排序

5-08 二分查找

六、树和树的算法

6-01 树的概念

6-02 二叉树的概念

6-03 二叉树的广度优先遍历

6-04 二叉树的实现

6-05 二叉树的先序、中序、后序遍历

6-06 二叉树由遍历确定一棵树